[PRML] 11장 표집법
개요
10장에서는 결정적 근사를 기반으로한 추론 알고리즘을 배웠다면, 이번 장에서는 수치적 표집법에 기반을 둔 근사 추론법인 Monte Carlo 테크닉에 대해 다룬다.
운이 좋다면 latent variable에 대한 사후분포를 직접적으로 구할 수 있겠지만 사실은 대부분의 경우 분포의 기댓값 정보만 필요로 한다. 따라서 이번 장에서는 기댓값만 관심을 가져보자. 연속 변수일 때는 다음과 같이 기댓값이 표현된다(이산일 때는 sum으로)
\[E[f] = \int f(z)p(z)dz\]이번 단원에서는 이 적분을 구하기 복잡한 상황에서 어떻게 표집법을 활용해 기댓값을 얻어낼 것인지에 대해 다루는데, 이 idea는 분포 ${p(z)}$로 부터 독립적으로 표본 집합 ${z^{(l)}}$을 얻어내는 것에서 시작한다! 독립적으로 잘 뽑았다고 하면 다음과 같이 기댓값을 바꿔줄 수 있다. 물론 근사치이다.
\[\hat{f} = \frac{1}{L}\sum_{l \in L}{f(z)^{(l)}}\]이 추정량의 분산은 공식에 의해 다음과 같이 나타낼 수 있다.
\[var[\hat{f}] = \frac{1}{L}E[(f-E[f])^2]\qquad{(11.3)}\]놀라운 점은 실제로 10~20개 정도의 샘플로 기댓값을 꽤 정확하게 얻어낼 수 있다고 한다. 다만 당연하게도 이 샘플들을 독립적으로 얻어내는 것이 중요하다.
방향성 그래프(directed acyclic graph)의 경우 8장에서 다룬 ancestral sampling 기법을 단순히 적용해주면 될 것이다.
그런데, observed node가 존재할 경우 어떻게 할까? 생각해볼 수 있는 가장 단순한 방법은 똑같이 ancestal sampling을 사용하되, 관찰값과 다를 경우 버리고 같을 경우에만 가져가는 방식을 취해주는 방식이다. 물론 observed node들이 늘어날 수록 버리는 경우가 늘어나기 때문에, 실제로 잘 쓰이지는 않는다.
11.1 기본적인 표집 알고리즘
가장 단순한 방법으로 내장된 rand 함수를 통해 쉽게 구현할 수 있는 방법을 소개한다. 여기서 rand 함수가 독립적인 난수를 생성한다고 가정하자. 사실은 그렇지 않다고 알려져 있다.
11.1.1 표준분포
단일 변수 확률 분포 ${p(z)}$가 존재할 때 어떻게 표집하면 분포를 따라갈 수 있을지 생각을 먼저해보자.
당연하게도 확률이 높은 부분일 수록 많이 뽑히고, 적은 부분일 수록 적게 뽑혀야할 것이다. 확률 분포(pdf)의 누적 확률 분포(cdf)를 생각해보면, 높은 확률을 가지는 구간에서는 높은 기울기를 가질 것이다. 그렇다면 여기서 어떻게 추출하면 될까? cdf는 0~1의 함숫값을 가지고 있다는 사실로부터 힌트를 얻을 수 있다. 바로 cdf의 y축(0~1)에서 random sampling을 해주면 될 것이다.즉, 역함수의 정의역에서 샘플을 취해주면 된다는 것이다. 느낌으로는 꽤나 직관적인데 이를 증명해보면 아래와 같이 간단히 나타낼 수 있다.
\[since \quad F^{-1}(u) = inf\{x \mid F(x) \geq u\} \quad \forall u \in [0,1]\] \[P(F^{-1}(U) \leq x) = P(Y \leq F(x)) = F(x)\]마지막 등호는 ${U}$가 uniform하기 때문에 성립한다.
따라서 ${F^{-1}(U)}$의 cdf는 ${F(x)}$와 같은 분포이며, continuous pdf와 cdf는 1to1 correspondence가 보장되므로 증명이 완료된다.
단일변수에 대해 다뤘으므로 다변수에 대해서도 다룰 수 있는데, 독립 변수의 경우에는 단일 변수일 때와 마찬가지로 각각에 대해 inverse cdf를 구해서 sampling을 진행하면 된다. 책에서는 gaussian integral을 활용한 다변수 분포의 간소화 예시인 Box-Muller Method를 소개하는데, 마치 모든 다변수에서 그러는 것처럼 설명되어 있다.
uniform한 ${U_1, U_2}$가 주어져있을 때, Gaussian 분포를 따르는 ${z_1, z_2}$를 어떻게 구할지 생각해보자(이부분은 굳이 안봐도 될듯).
첫번째 방법
앞서 설명한 가장 단순한 방법은 각자 inverse cdf를 구해주는 방법이다. cdf는 다음과 같다.
\[F(z)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{z}\exp\left\{-\frac{u^2}{2}\right\} du\]inverse를 구해주면, 아래와 같다. erfinv는 여기를 참고
\[F^{-1}(U) = \sqrt{2}\: \textbf{erfinv} (2U-1)\]여기서 ${U_1, U_2}$를 사용해 각 ${z_1, z_2}$를 구할 수 있다.
두번째 방법
erf는 anayltic하지 않은 영 좋지 않은 함수이기에 gaussian integral에서 배운 극좌표 변환 테크닉을 이용해 간단해질 수 있다. ${z}$를 2차원 평면에 두고 ${U}$들이 ${r}$과 ${\theta}$를 표현하도록 적절히 변환해주면 될 것이다. 그 과정은 아래와 같다.
\[\begin{aligned}f(z_1, z_2) &= f(z_1)f(z_2) \\ &= \frac{1}{\sqrt{2\pi}} \exp \left\{-\frac{z_1^2}{2}\right\} \frac{1}{\sqrt{2\pi}} \exp \left\{-\frac{z_2^2}{2}\right\} \\ &= \frac{1}{2 \pi} \exp \left\{\frac{z_1^2 + z_2^2}{2}\right\} \end{aligned}\]여기서 아래와 같이 둔다.
\[z_1 = \sqrt{2} s \cos(\theta) \\z_2=\sqrt{2} s\sin(\theta)\]그러면, 아래와 같이 단순해진다.
\[f(z_1,z_2) = \frac{1}{2\pi}e^{-s}\]즉 두 pdf의 곱으로 생각할 수 있고 각각에 대해 inverse cdf를 구해주면 다음과 같다.
\[\begin{aligned}\theta &= 2\pi U_1 \\ r &= -\ln(1-U_2)\end{aligned}\]즉, 우리의 목표인 ${z_1, z_2}$는 다음과 같이 구해진다.
\[z_1 = \sqrt{-2\ln(U_1)} \cos (2\pi U_2) \\ z_2 = \sqrt{-2\ln(U_1)} \sin (2\pi U_2)\]uniform 만 잘 뽑혔다면 두 방법은 완전히 같은 결과를 보여준다.
이번 경우는 운이 좋은 경우였고, 그렇지 않은 경우들에 대해 일반적인 방법이 필요하다. 특별히 단변량 분포에 대해서는 rejection sampling과 importance sampling 기법이 있는데 이에 대해 알아보자.
11.1.2 거부 표집법 (Rejection Sampling)
일반적인 분포 ${p(z)}$에서 표집을 할때 사용하는 간단한 기법이다.
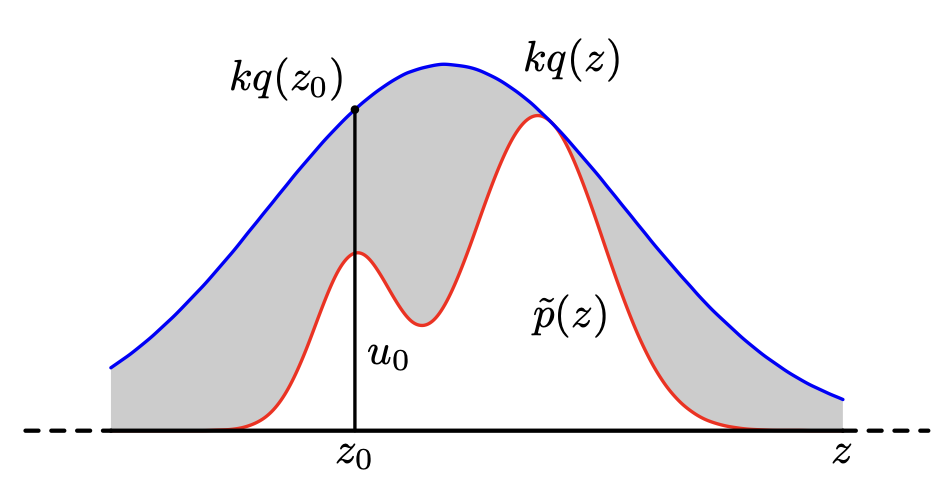
- ${p(z)}$와 개형이 최대한 비슷한 적절하게 해석적인 함수 ${q(z)}$를 잡는다.
- 모든 구간에서 ${kq(z) \geq p(z)}$를 만족하는 상수 ${k}$를 구한다. 작을수록 좋다!
- ${q(z)}$를 앞서 배운 방법들로 sampling해 ${z_0}$를 얻는다.
- 구간 ${[0, kq(z_0)]}$에서 uniform sampling을 해 ${u)0}$를 얻는다.
- 만약 ${u_0 > p(z)}$면 버리고(reject) 그렇지 않다면 유지한다.
11.1.3 적응적 거부 표집법
적절한 ${q(z)}$를 찾는것이 어려울 경우를 위한 방법(야매)이다.
먼저, ${\ln(p(z))}$가 오목함수인 경우에는 단순히 line interpolation method로 해결이 가능하다. numerical analysis 첫시간에 배우는 무식한 방법이지만 빠르고 좋은 방법이다. 여기서도 볼줄이야. 당연히 수집하는 point의 수가 늘어날 수록 ${p(z)}$와 ${q(z)}$가 비슷해질 것이며 rejection rate도 줄어들 것이다.
- 각 point에서 미분이 정의되지 않는데 변형 알고리즘이 존재한다고 한다.
- 로그 오목이 아닐경우 11.2.2에서 살펴본다. aka Adaptive Rejection Metropolis Sampling
- 고차원 공간에서는 acception rate가 기하급수적으로 감소하기 때문에 이를 개선하기 위해 복잡도가 급격히 증가하기에 사용하기 어렵다.
11.1.4 중요도 표집법
역시 표집하기 어려운 분포가 주어졌다고 가정하고 기닷갮 ${E(z)}$를 구해보자.
이번에도 새로운 분포 ${q(z)}$를 두고 일단 샘플링을 해서 ${z^l}$들을 얻어내고 해당 ${z^l}$에서 ${\frac{p(z)}{q(z)}}$만큼의 weight를 주고 기댓값을 계산해주는 방식이다. 기본 idea는 Rejection Sampling과 다를바 없어 보인다.
논리대로 식을 전개해보자면 다음과 같다.
\[E[f] = \int f(z)p(z)dz = \frac{Z_q}{Z_p}\int f(z)\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \simeq \frac{Z_q}{Z_p}\frac{1}{L} \sum_{l=1}^{L} \tilde{r}_{l} f(z^{(l)})\]마찬가지로 ${q(z)}$가 얼마나 ${p(z)}$와 비슷한 분포를 가지는지, ${p(z)}$의 자연스러운 분포 여부(적당히 생긴)에 따라 기댓값의 정확도가 상승한다.
- 그래프 모델에서는 여기에 마르코프한 가중치를 덮어주면 된다. 또한, 이를 발전시킨 형태로 Likelihood Weighted Sampling(가능도 가중 표집법)이 존재한다. 이는 Ancestral Sampling(조상 표집법)을 적용한 형태로 진행. 더 나아가 Self Importance Sampling(자가 중요도 표집법)도 있는데 그만 알아보자.
11.1.5 표집 중요도 재표집
Rejection Sampling을 할때 ${k}$를 구하는 과정이 있었는데, 이 과정을 생략해주는 방법이다.
- ${q(z)}$로부터 ${z^l}$을 추출한다.
- 각 ${z^l}$에 대한 가중치 ${w_l}$을 계산한다.
- 각각의 확률이 ${w_l}$을 가지는 이산 분포 ${z^l}$들로부터 다시 ${L}$개를 추출한다.
결국 Rejection Sampling에 Importance Sampling을 덮어준 형태인데, 기본 idea는 같은 것이라 크게 발전된 형태로 보이지는 않는다.
11.1.6 표집법과 EM 알고리즘
EM을 사용할 때, E단계에서 non-analytic한 함수를 만났을 경우 표집법을 통한 근사로 해결이 가능하다.
즉, 적분꼴로 표현된 최적화 대상을 이산 합 형태로 아래와 같이 바꿔주는 것이다.
\[Q(\theta, \theta^{old}) = \int p(\textbf{Z} | \textbf{X} , \theta^{old}) \ln p(\textbf{Z},\textbf{X} | \theta) \, d\textbf{Z}\] \[to\] \[Q(\theta, \theta^{old}) \approx \frac{1}{L} \sum \ln p(\textbf{Z}^{(l)}, \textbf{X} \bar \theta )\]이 과정을 Monte Carlo EM algorithm이라고 부른다.
참고) IP 알고리즘
${p(\textbf{Z} \mid \textbf{X})}$에서 표집이 어려운 상황에서 Maximum Likelihood 대신 Bayesian하게 접근해서 해결하는 방법.
- I Step
순서대로 ${\textbf{X}}$로부터 ${\theta ^{(l)}}$들을 추출하고 이들의 결합분포를 통해 ${p(\textbf{Z} \mid \textbf{X} , \theta)}$에서 ${\textbf{X}}$를 추출한다.
- P Step
구한 ${\textbf{Z}}$들을 통해 ${\theta}$에 대한 사후분포식을 수정해준다.
11.2 마르코프 연쇄 몬테 카를로
MCMC는 Rejection Sampling이나 Importance Sampling과 비슷한 방식으로 진행되지만, 무조건 Reject되기 보다는 회생의 기회를 준다는점에서 차이가 있다. 물론 여기서 얻은 표본들도 독립이 아니지만, 충분히 큰 M에 대해 kM번째 샘플만 취해준다면 어느정도 독립성을 보장해줄 수 있다.
먼저, 가장 대표적인 방식인 Metropolis Algorithm에 대해 알아보자.
- 목표 분포 ${p(z)}$에 대해 Rejection Sampling때와 마찬가지로 적절한 ${q(z)}$를 잡아준다. (Metropolis 알고리즘에서는 대칭(${q(z_A \mid z_B) = q(z_B \mid z_A)}$)임을 가정한다.)
- 초깃값 ${z^{(1)}}$을 시작으로 ${q(z)}$ 에서 하나의 표본 ${z^*}$을 추출한다.
- Accept or Reject
- ${p(z^*) > p(z^{(1)})}$일경우 accept
- 그렇지 않을 경우, $\frac{p(z^*)}{p(z^{(1)})}$의 확률로 accept한다.
- 이를 다시표현하면, ${min \left(1, \frac{p(z^*)}{p(z^{(1)})}\right)}$의 확률로 Accept한다.
이에 대한 증명은 적혀있지 않은데, 11.2.2에서 일반화된 증명으로 살펴본다.
11.2.1 마르코프 연쇄
다음 상태가 현재 상태에만 의존할 경우 마르코프하다고 한다.
\[{ p(z^{(m+1)} \mid z^{(1)}, \ldots z^{(m)}) = p(z^{(m+1)}\mid z^{(m)} )}\]각 상태에서 ${T_{m}^{ij} = p(z^{(m+1)} = v_j \mid z^{(m)} = v_i) }$을 Transition Matrix라고 부르며 이 matrix가 ${m}$에 무관할 경우 Homogenous한 chain이라고 부른다.
최종적으로 ergodic 개념이 중요한데, 아래 세 조건은 동치이다.
- Ergodic
- Positive Recurrent, Aperiodic
- Finite, Irreducible, Aperiodic
즉, ergodic하면, 충분한 시간이 흐른 뒤 분포와 초기 분포가 동일한 분포가 된다.
또한, 헷갈리는 개념으로 stationary가 있는데, transition matrix ${T}$에 대해 ${\pi = \pi T}$를 만족할 때, 즉, 분포가 일정할 때 stationary(invariant)하다고 한다.
\[p(z^{(m+1)}) = \sum p(z^{(m+1)} \mid z^{(m)}) p(z^{(m)})\]일반적으로 ergodic하면 stationary한 ${\pi}$가 존재하며 stationary하다.
자세한 내용이 궁금하다면 Stochastic Process를 공부해보자. 재밌는 책이다.
11.2.2 메트로폴리스 헤이스팅스 알고리즘
앞선 Metropolis Algorithm은 대칭 ${q(z)}$만을 사용했는데, 한계가 있으므로 이번에는 좀더 일반적인 상황을 위한 해법을 살펴보자.
유일한 차이는 Accept or Reject할 때이다. 다음과 같이 acceptance rate를 정규화해주면 된다.
\[rate_{z, z'} = min\left(1, \frac{\frac{p(z^*)}{q(z^* \mid z^m)}}{\frac{p(z^m)}{q(z^m \mid z^*)}} \right)\]이제 이렇게 얻은 표본집합이 ${p(z)}$에 수렴한다는 것을 증명해야한다. 책에는 좀 대충나와있는 것 같다.
일단, 각 표본들은 위의 rate를 따르는 MC라고 볼 수 있다. 나아가, acceptance rate를 통해 postivie recurrent함을 확인할 수 있고, 당연하게 Aperiodic하므로, Ergodic한 MC임을 쉽게 볼 수 있다. 따라서, unique한 stationary matrix ${\pi}$를 가짐을 알 수 있다. 이제, ${\pi}$가 ${p(x)}$에 수렴함을 보여야한다. 다음 식을 살펴보자.
\[\begin{aligned}p(z)q(z'\mid z) * rate_{z, z'} &= min\left(p(z)q(z'\mid z), p(z')q(z\mid z')\right) \\ &= min\left(p(z')q(z\mid z'), p(z)q(z'\mid z)\right) \\ &= p(z')q(z\mid z') * rate_{z', z}\end{aligned}\]따라서, ${q(z)}$와 rate의 결합은 이 MC의 transition probability라고 볼 수 있으며, 결국 같은 ${\pi}$에 수렴함을 알 수 있다.
마찬가지로, 어떤 ${q(z)}$를 사용하는지에 따라 알고리즘의 성능에 현저한 영향을 줄 수 있다. 일반적으로 gaussian을 사용한다. 여기서 분산을 어떻게 두냐에 따른 trade-off가 있는데, 분산이 작을 경우 acceptance는 증가하지만, 전체를 탐색하기 오래걸리고, 분산이 클 경우 acceptance 자체가 낮아지게 된다. 따라서 그림 11.10과 같이 방향에 따라 분산의 차이가 클 경우 알고리즘이 느리게 수렴하게 된다.
11.3 깁스 표집법
알고보니 Gibbs Free Energy를 정의한 그 Gibbs이다. 이쪽업계 코시 같은 사람인듯;
아무튼 Gibbs Sampling은 MCMC의 한 종류이다. 방법은 간단한데, ${m}$개의 확률변수들이 결합된 결합확률분포가 있을 때, ${m - 1}$개의 변수를 고정시키고 남은 한개를 조건부 확률분포로 부터 표집하고, 다른 ${m-1}$개를 고정시키고 남은 한개를 표집하고 … 을 반복해서 얻어나가는 방법이다. 너무 rough하게 적은것 같으니 좀더 정확하게 설명하면 ${T}$회 반복하는 경우 아래와 같다.
- initialize ${z_i : i = 1, \ldots M}$
- for ${i}$ in range (${1}$, ${T}$)
- ${p(z_1 \mid z_2^{i},z_3^{i},\ldots,z_M^{i})}$에서 ${z_1^{i+1}}$을 표집한다.
- ${p(z_2 \mid z_1^{i+1},z_3^{i},\ldots,z_M^{i})}$에서 ${z_2^{i+1}}$을 표집한다. ${\vdots}$
- ${p(z_M \mid z_1^{i+1},z_2^{i+1},\ldots,z_{M-1}^{i+1})}$에서 ${z_M^{i+1}}$을 표집한다.
여기서는 변수들에게 order를 부여하고 진행했는데, random한 order로 진행할 수도 있다. 물론 결과적으로는 같다.
이제, 이 기법이 올바른 샘플링임을 증명해보자. MH 알고리즘의 일종이라고 언급했으니 이게 왜 MH 알고리즘인지 증명해보면 된다. 좀 rough하게 살펴보자.
일단, 이 분포 또한 MH에서 사용한 분포와 같이 stationary함을 보여야한다. 이는 꽤나 자명한데, 각 표집에서 적절한 조건부 분포를 사용하기 때문이다. 즉, 적할한 ${\pi}$가 존재한다.
\[\begin{aligned} rate &= min\left( 1, \frac{p(z^*)q(z|z^*)}{p(z)q(z^*|z) } \right)\\ &= min\left(1, \frac{p(z^*_k|z^*_{-k})p(z^*_{-k})p(z_k | z^*_{-k})}{p(z_k|z_{-k})p(z_{-k})p(z^*_{k}|z_{-k})} \right) \\ &= min(1,1) = 1\end{aligned}\]즉, MH와 같은 rate를 가지고 있기 때문에, MH의 일종으로 볼 수 있다.
11.4 조각 표집법
계속해서 보이는 알고리즘들의 단점은 ${p(z)}$와 ${q(z)}$의 차이에서 비롯되었다. 분산이 작으면 탐색이 느리고, 크면 acceptance가 낮아진다. 조각표집법(slice sampling)은 새로운 방식으로 해결하고자 했다.
아이디어는 간단한데, 아래와 같이 y축에서 쳐다보는 변수 ${u}$를 추가해서 해결하는 것이다.
\[\hat p(z,u) = \begin{cases} 1/Z_p & 0 \leq u \leq \hat p(z) \\ 0 & else \end{cases}\]그리고, 깁스 샘플링 같은 방법을 통해 ${\hat p(z,u)}$에서 표본을 얻고, ${u}$를 무시해주어 원 분포를 얻는 방식이다.
근데 이건 그냥 원래 있던 inverse cdf하는 방법보다도 원시적인 방법이 아닌가 싶다.
Leave a comment